Japanese / English
Updated - April 2, 2024 -
My Hobby (Music) => Click!
Lab. Website => Click!
Click the movie to play.
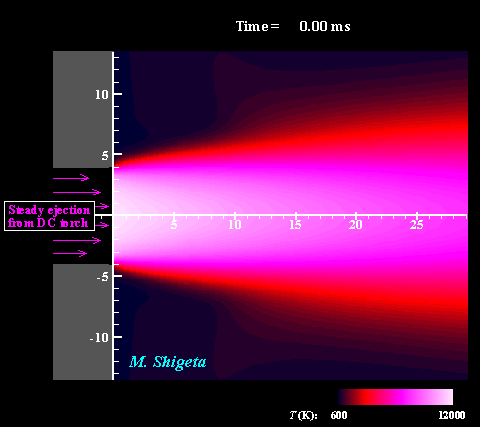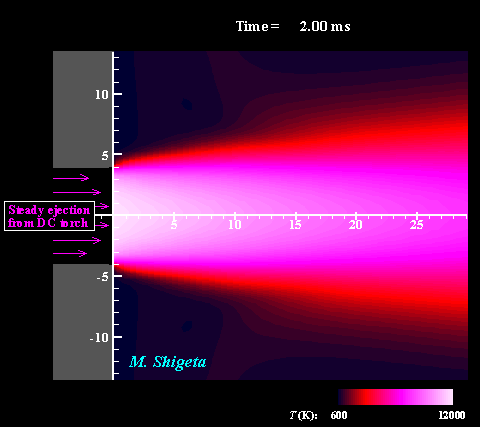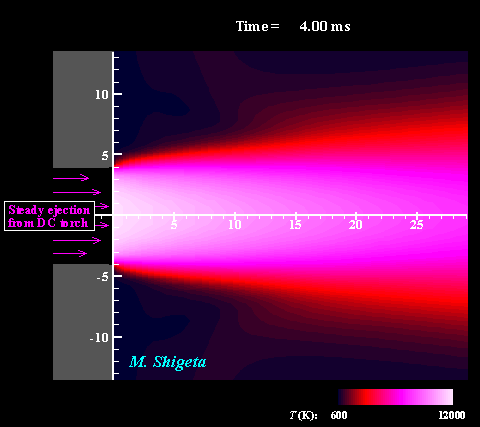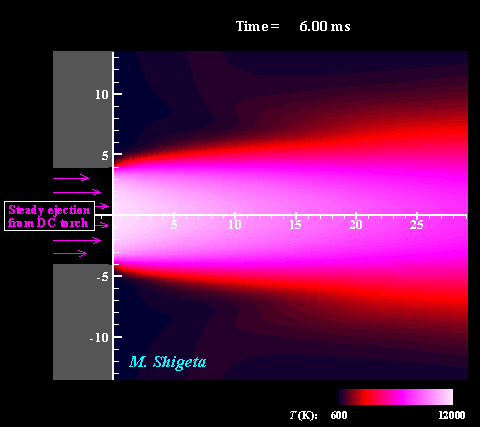
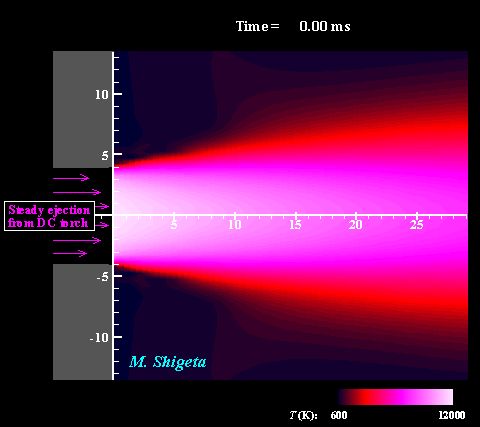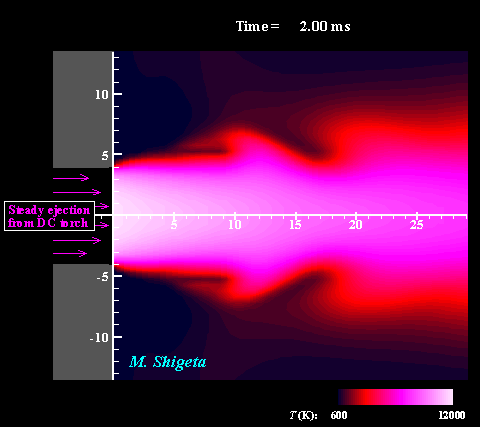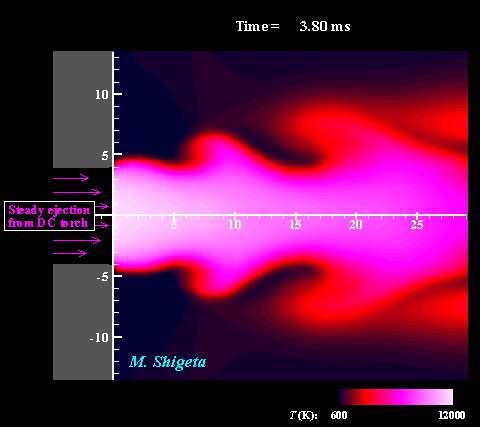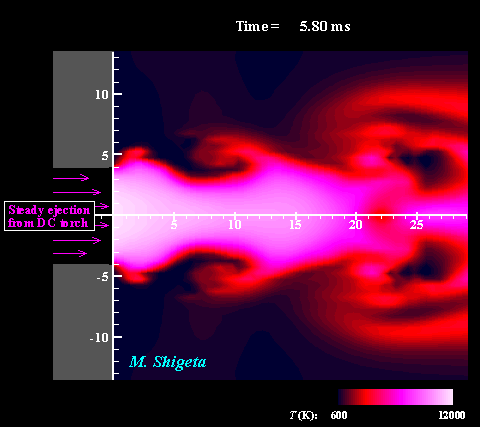
Three-dimensional flow dynamics of a DC-RF hybrid thermal plasma
|
A strong and useful plasma field is obtained by combining a radio-frequency (RF) inductively coupled thermal plasma and a non-transferred direct current (DC) thermal plasma jet. However, a thermal plasma is a unique fluid with intense light emission, high temperature (over 10,000 K), a complicated flow caused by electromagnetic forces and thermal expansion. This feature prevents direct measurements in experiments; therefore, the details of the thermofluid field are still poorly understood. A time-dependent 3-D simulation based on magnetohydrodynamics (MHD) has been attempted to clarify the thermofluid field of the plasma, which is governed by the conservation equations of mass, momentum (Navier-Stokes) and energy coupled with the electromagnetic equations (Maxwell). Simultaneously, the simulation takes account of the temperature-dependent large variations of the thermodynamic and transport properties as a plasma "fluid". The movies show the dynamic behaviors of the thermofluid field and the vortex structure interacting with the electromangeitc field. The colors indicate the temperatures. Such a complicated flow has been predicted from experimental studies; however, it has never been obtained by any axisymmetric 2-D simulations which have been carried out. The present time-dependent 3-D simulation has first successfully obtained these realistic results and revealed the plasma flow dynamics. (Note: Some careful treatments are required to capture vortex structures of thermal plasma flows by numerical simulation. See the next section.) For more information, please see ... Journal of Physics D: Applied Physics, Vol. 46, No. 1, (January, 2013) 015401 (12 pages). Masaya Shigeta Plasma Sources Science and Technology, Vol. 21, No. 5, (October, 2012), pp. 055029 (14 pages). Masaya Shigeta Journal of Physics D: Applied Physics, Vol. 49, No. 49, (November 9, 2016), pp. 493001 (18 pages). Masaya Shigeta |
Click the movie to play.
Fundamental problem in numerical simulation of thermal plasmas


|
As mentioned the above section, simulation of thermal plasma is generally difficult. The entire flow field, in which the plasma at a high temperature and a cold gas at room temperature co-exist, must be treated simultaneously. Widely varied temperatures of 300-12,000 K cause large variations of the transport properties and the density. Meanwhile, the Mach numbers are very small in and around the plasma. Consequently, when a numerical method for a compressible flow simulation is used, the computation takes an extremely long time to obtain a numerical solution for a practical time scale. Therefore, a thermal plasma is treated as an incompressible flow with the density as a temperatur-edependent variable. This condition, which is severe for numerical flow simulations, usually destabilizes the computation (= the computation easily breaks down). That is why thermal plasma simulations have often used differencing schemes which suppress numerical instability effectively. However, those schemes also suppress the actual physical instability simultaneously. In consequence, the numerical result does not simulate any realistic flow with vortices as shown in Left figure. On the other hand, schemes that are effective for vortex capturing often cause destabilization of computations. Although these two aspects mutually conflict, thermal plasma flows should also be calculated as "simulation" somehow using such schemes to obtain realistic results. As a result, the effort gives a more realistic flow as shown in Right figure. An experiment visualized that a thermal plasma jet entrained surrounding cold gas by Kelvin-Helmholtz instability about 30 years ago. Nevertheless, such a flow had never been simulated because of the numerically severe conditions. Overcoming the difficulties, the present effort broke through that problem and obtaiend a successful result. For more information, see ... Journal of Physics D: Applied Physics, Vol. 49, No. 49, (November, 2016), pp. 493001 (18 pages). Masaya Shigeta IEEJ Transactions on Electrical and Electronic Engineering, Vol. 14, (January 1, 2019), pp. 16-28. Masaya Shigeta Plasma Chemistry and Plasma Processing, Vol. 40, Issue 3, (May 1, 2020), pp. 775-794. Masaya Shigeta [ New!! ] 3D simulation => Click! |
Simple equations to describe aerosol growth
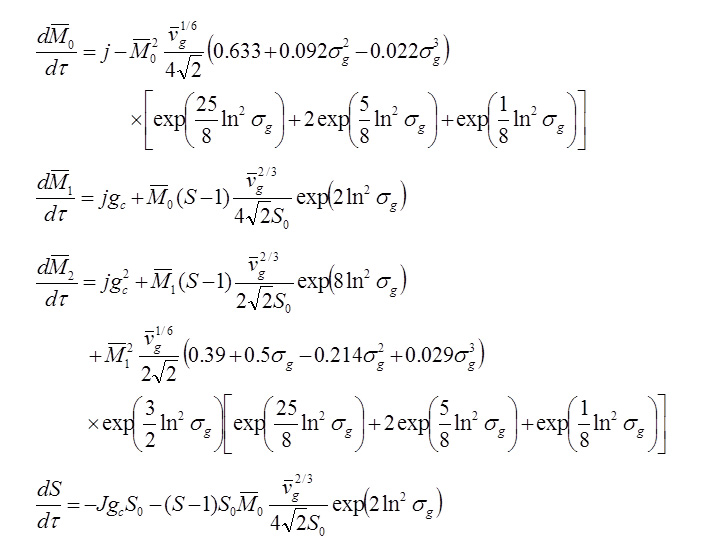
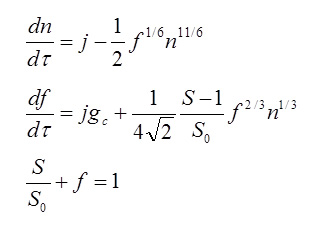
often-used equations of moments our new equations
|
Both sets of equations give almost the same results for the time evolutions of the particle number density and mean size of aerosol. Aerosol growth through nucleation, condensation/evaporation and coagulation has usually been described by the simultaneous equations of the moments of the particle size distribution function (PSDF) with its profile assumption (Left) in numerical calculations. This method solves the four complex ordinary differential equations. For this problem, we derived a set of two ordinary differential equations and one algebraic equation (Right) without any profile assumption for the PSDF. In spite of its much simpler formulation and lower computational costs, it gives reasonable a numerical result which is almost the same as that obtained with a more complex set of equations (Left). This mathematical model can be expected to be applied to numerical predictions for not only plasma-aided nanopowder syntheses but also water-droplet generation in a steam turbine (causing erosion), meteorological problems with cloud/fog generation, space design requiring humidity control, etc. Note that the paper below presents the sets of equations applicable to the continuum size regime as well as the free molecular size regime shown above. For more information, see ... Modelling and Simulation in Materials Science and Engineering, Vol. 20, No. 4, (May, 2012), pp. 045017 (11 pages). Valerian A. Nemchinsky and Masaya Shigeta IEEJ Transactions on Electrical and Electronic Engineering, Vol. 14, (January 1, 2019), pp. 16-28. Masaya Shigeta Plasma Chemistry and Plasma Processing, Vol. 40, Issue 3, (May 1, 2020), pp. 775-794. Masaya Shigeta [ New!! ] 3D simulation => Click! |
Click the movie to play.
Collective growth of silicide nanoparticles (nanopowder) in thermal plasma synthesis
|
These movies show the time evolutions of the particle size-composition distributions of the silicide (metal-silicon intermetallic compound) nanoparticles (nanopowder) synthesized in thermal plasma processing. We have successfully clarified the formation mechanisms including binary nucleation and binary co-condensation of two components (Mo&Si, Co&Si, etc.) by our original mathematical model and solution algorithm "Two-Directional Nodal Method". In Mo-Si system (Initial vapor ratio Mo:Si = 1:1), the molybdenum-rich nanoparticles first grow up and subsequently silicon condenses on the nanoparticles, which results in the significant growth of the nanopowder. On the other hand, in Co-Si system (Initial vapor ratio Co:Si = 1:1), silicon-rich nuclei are first generated and immediately make a rapid growth into nanoparticles due to simultaneous co-condensation of cobalt and silicon. These results show that the nanopowders synthesized in thermal plasma processing have widely ranging sizes and compositions inevitably even under a simple condition (Initial vapor ratio Metal:Si = 1:1). These numerical results agree with the experiment results, which endorses the validity of our model. In addition to molybdenum-silicide (Mo-Si) and cobalt-silicide (Co-Si), the nanoparitcles' formation mechanisms are being studied for titanium-silicide (Ti-Si), iron-silicide (Fe-Si), borides (boron-based intermetallic compound), and magnetic alloys (Fe-Co, Fe-Nd etc.). For more information, see ... Journal of Applied Physics, Vol. 108, Issue 4, (August, 2010), pp. 043306 (15 pages). Masaya Shigeta and Takayuki Watanabe Powder Technology, Vol. 288, (January 1, 2016), pp. 191-201. Masaya Shigeta, Takayuki Watanabe Nanomaterials, Vol. 6, (March 7, 2016), pp. 43 (10 pages). (Impact factor = 3.553, 5-year impact factor = 4.100) Masaya Shigeta, Takayuki Watanabe |
Click the movie to play.
Radio-frequency inductively coupled thermal plasma flow
& nanoparticle formation with counterflow cooling
|
It is possible to mass-produce nanoparticles by quenching a thermal plasma flow including material vapor (here, platinum vapor) with counterflow cooling promoting nucleation. These numerical results can be obtained by solving the mathematical models coupling the sequential physics of a plasma flow dynamics, material vaporization, and nanopowder growth. Nanoparticles are created through homogeneous nucleation and subsequent heterogeneous condensation growth. The nanoparticles simultaneously grow up by Brownian coagulation between themselves. However, it is still impossible to calculate this collective growth of many nanoparticles for a practical time scale by the "Molecular dynamics" approach even with powerful computers. Meanwhile, an "Aerosol dynamics" equation effectively expresses the growth. Although the equation cannot be solved even numerically yet, it can be calculated by combining with a statistical method. In addition, the calculation also takes into account diffusion, thermophoresis, and convection of nanoparticles as well as transport of material vapor. Many nuclei are generated at the interface between the plasma flow and the counterflow. Being transported downstream, the nuclei grow up into nanoparticles gaining the material vapor. The nanoparticles also increase their sizes by coagulation with each other, and consequently the number of nanoparticles decreases. For more information, see ... Journal of Applied Physics, Vol. 103, Issue 7, (April, 2008), pp. 074903 (15 pages). Masaya Shigeta and Takayuki Watanabe Thin Solid Films, Vol. 516. (May, 2008), pp. 4415-4422. Masaya Shigeta and Takayuki Watanabe Transactions of the Japan Society of Mechanical Engineers, Vol. 75, No. 758, (October, 2009), pp. 2019-2028. (in Japanese) Masaya Shigeta and Takayuki Watanabe |
Click the movie to play.
Arc plasma dynamics in a TIG welding condition
|
This movie shows a simulation result of arc plasma in a TIG welding condition. The arc plasma has Max. temperature ~18000 K and Max. speed ~200 m/s beneath the electrode tip. However, their positions do not coincide. It is also interesting that the sizes of the high-temperature region and the high-speed region are different. The shielding gas supplied from the top is entrained partially into arc plasma, ionized, and then becomes arc plasma. The high-temperature region is almost stationary whereas the low-to-middle-temperature region fluctuates by fluid dynamic instability. For more information, see ... Nanomaterials, Vol. 9, No. 12, (December 6, 2019), pp. 1736 (13 pages). (OPEN ACCESS) Masaya Shigeta, Manabu Tanaka, Emanuele Ghedini |
Click the movie to play.
Dynamics of two non-neutral plasma rings in a uniform magnetic field
|
A dynamic motion of two non-neutral plasma rings in a uniform magnetic field was simulated using a discrete vortex method with a symplectic integrator. Finite Larmor radius effect and Transient electric field effect were taken into account as well. Here, electron plasma or positron plasma was supposed as a non-neutral plasma. Colors indicate the speeds in each system. (Movie loops 3 times.) |
Click the movie to play.
Vortex Generation & Merging of RF Induction Coupled Thermal Plasma & Off-Axis DC Thermal Plasma Jet
|
Electromagnetic thermofluid simulation of a coexisting system of direct current (DC) - radio frequency (RF) induction hybrid thermal plasma and non-ionized gas, which can realize mass production of nanoparticles, was performed. I have developed a method that can both capture hydrodynamic instabilities and numerically stable long-time calculations under the severe numerical conditions of solving incompressible flows with low Mach number in the same computational domain, where the physical properties and density change over several orders of magnitude with spatio-temporal changes in temperature from room temperature to over 10,000 K, and have successfully captured the dynamics of the thermal flow field and vortex structure. The results are consistent with the theoretical prediction that only large vortices exist in the high-temperature plasma region and small vortex clusters occur only in the low-temperature region. The vortex structure evolves into a more complex one after the merger of the off-axis DC plasma jet and the RF induction plasma through collision.
For more information, see ... Japanese Journal of Applied Physics, Vol. 62, (June 16, 2023), pp. SL0801. (OPEN ACCESS) Masaya Shigeta Journal of Physics D: Applied Physics, Vol. 49, No. 49, (November 9, 2016), pp. 493001 (18 pages). Masaya Shigeta Journal of Physics D: Applied Physics, Vol. 46, No. 1, (January, 2013), pp. 015401 (12 pages). Masaya Shigeta Plasma Sources Science and Technology, Vol. 21, No. 5, (October, 2012), pp. 055029 (14 pages). Masaya Shigeta |
Click the movie to play.
Flow dynamics and Nanopowder cloud behavior at plasma jet ejection
|
This is a simulation of a coexistent system in which an Ar plasma jet with an absolute temperature of 12000 K containing Si vapor is ejected into a nonionized Ar gas at a room temperature of 300 K. Fluctuations due to the Kelvin-Helmholtz instability are visualized by the complex dynamics of the thermofluid field caused by the interaction between the two and the clouds of Si nanoparticles generated in the boundary region with a very high temperature gradient of about 3000 K/mm. For more information, see ... Japanese Journal of Applied Physics, Vol. 62, (June 16, 2023), pp. SL0801. (OPEN ACCESS) Masaya Shigeta Plasma Chemistry and Plasma Processing, Vol. 40, Issue 3, (May 1, 2020), pp. 775-794. Masaya Shigeta |
© 2004- Masaya SHIGETA