Japanese / English
Updated - October 8, 2025 -
趣味(ドラム)のページは → こちら
研究室のサイトは → こちら
動画をクリックすると再生します
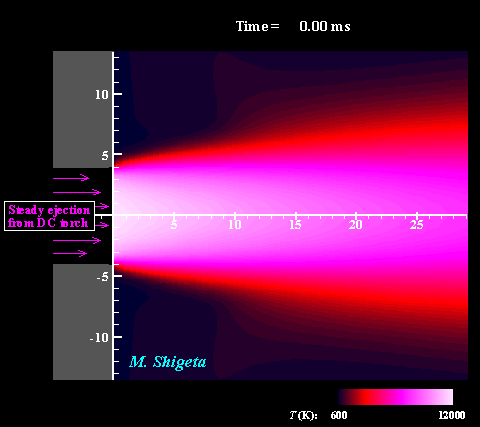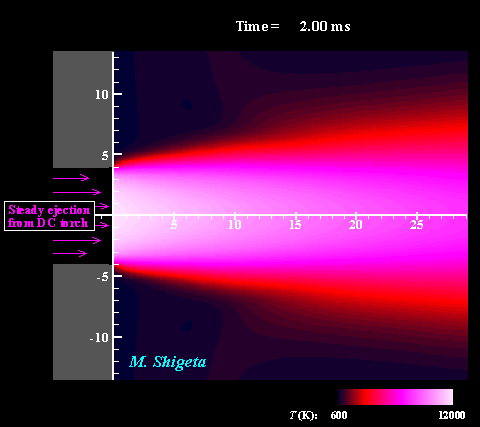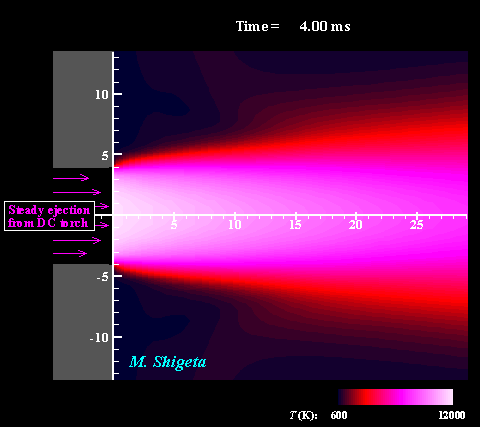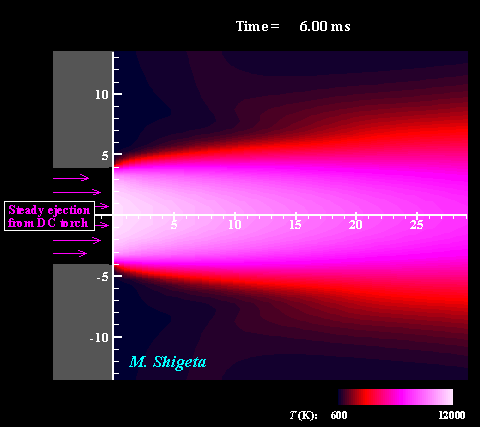
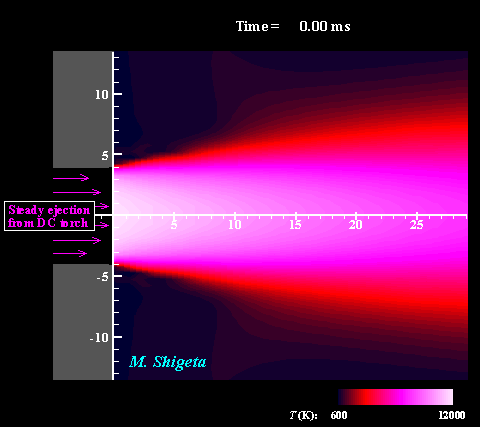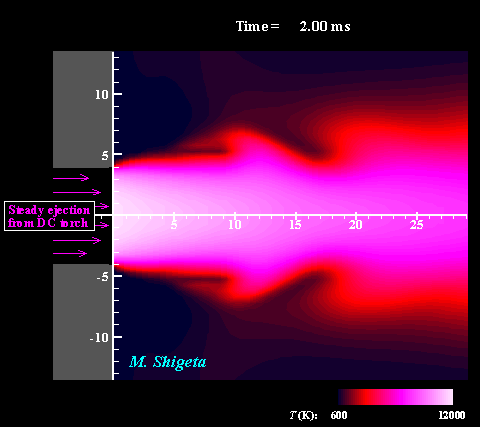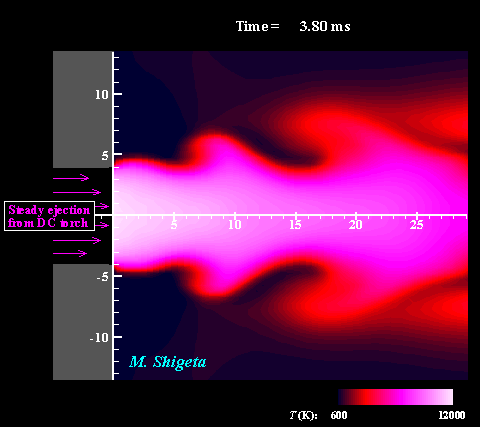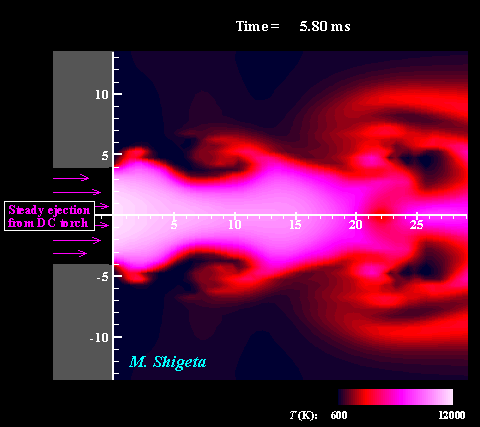
直流−高周波誘導ハイブリッド熱プラズマの3次元流動ダイナミクス
|
高周波(RF)誘導結合型熱プラズマに非移行式直流(DC)熱プラズマジェットと組み合わせることでプラズマ領域を補完することができます。しかし、熱プラズマは強い発光をともなう特殊な流体で、その温度が1万度に及ぶ上、電磁気力と熱膨張によって複雑な流れ場になっているため、実験による直接計測は難しく、熱流動現象の詳細は不明でした。 そこで電磁流体力学(MHD)に基づく非定常3次元数値シミュレーションによる現象の解明を試みました。現象を記述する方程式は、流体力学における連続の式、Navier-Stokes方程式、エネルギー方程式、電磁気学におけるMaxwellの方程式で、これらはプラズマ維持条件の下、すべて同時に数値的に解かれます。またプラズマが流体として持つ物性値や熱力学的特性が温度によって大きく変化する(数ケタ変わるものもある)効果も考慮されます。 動画は電磁場と相互作用する熱流動場および渦構造の動的な挙動を示しています。色は温度を表しています。このように非常に複雑な流れ場になっていることは、実験的研究によって示唆はされていたものの、それまで行われていた軸対称2次元シミュレーションでは全く予測できませんでした。この非定常3次元シミュレーションによって、より現実的な結果が得られ、現象の詳細が初めて明らかに示されたと言えます。 (注:数値計算によって熱プラズマ流の渦構造を捉えるためには配慮が必要です。下の項目をご覧ください。) ※ 詳しくはこちら(↓)をご参照ください。 Journal of Physics D: Applied Physics, Vol. 46, No. 1, (January, 2013) 015401 (12 pages). Masaya Shigeta Plasma Sources Science and Technology, Vol. 21, No. 5, (October, 2012), pp. 055029 (14 pages). Masaya Shigeta Journal of Physics D: Applied Physics, Vol. 49, No. 49, (November 9, 2016), pp. 493001 (18 pages). Masaya Shigeta |
アニメーションが止まっている場合は
ページをブラウザ上で「更新」してください
熱プラズマ流の数値計算における基本的な問題


|
上の項目でも述べましたが、熱プラズマ流の数値計算では室温〜1万度超という大きな温度の時空間変化を同じ計算領域内で取り扱わなければなりません。同時に温度変化に伴う物性値や密度の変化も考慮に入れる必要があります。 一方でマッハ数は小さく、渦の動的挙動をシミュレートするためには、圧縮性流体用の計算スキームでは非常に長い計算時間を要してしまいますので、非圧縮性流体用の計算スキームを用いることが現実的となります。しかしこれは数値流体計算において“とても過酷な条件”で、計算は容易に破綻してしまいます。そのため、これまでの熱プラズマシミュレーションでは解を得るために計算を安定に行うことのできる差分スキームが用いられてきました。ところがそのようなスキームは計算を安定化すると同時に物理的な不安定性も抑制してしまうため、得られる結果は左図のように渦運動が全く再現されないものとなってしまいます。一方で、渦運動を伴う現実的な流体運動を再現するためには(熱プラズマのような過酷な計算条件において解を得るには大きな労を要しますが)やはり渦運動の捕捉に適した差分スキームを用いる必要があります。そのようにして得られた結果が右図です。 熱プラズマジェットが Kelvin-Helmholtz不安定性によって周囲の低温気体を巻き込むことは30年ほど前に実験により示されました。それにも関わらず、これまで数値計算によって再現されたという報告がなかったのは上記の理由によるところですが、ようやく成功したと言えます。 ※ 詳しくはこちら(↓)をご参照ください。 Journal of Physics D: Applied Physics, Vol. 49, No. 49, (November, 2016), pp. 493001 (18 pages). Masaya Shigeta IEEJ Transactions on Electrical and Electronic Engineering, Vol. 14, (January 1, 2019), pp. 16-28. Masaya Shigeta Plasma Chemistry and Plasma Processing, Vol. 40, Issue 3, (May 1, 2020), pp. 775-794. Masaya Shigeta 【 New!! 】3次元シミュレーションの結果は → こちら |
エアロゾルの成長を簡潔に記述する方程式系の提案
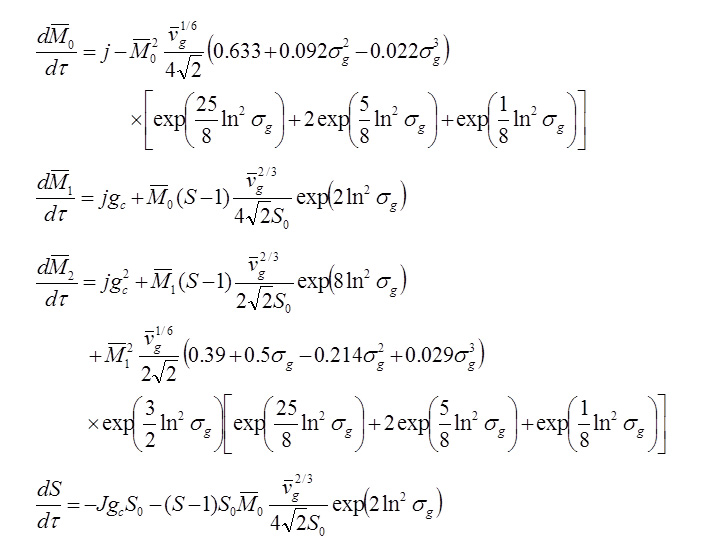
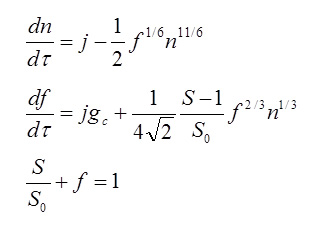
従来の方程式系 提案した方程式系
|
エアロゾルの粒子数密度や平均粒径の時間変化について、両者は ほぼ"同じ結果" を与えてくれます。 これまで 均一核生成・不均一凝縮・粒子間凝集を経るエアロゾルの成長過程は、粒度分布関数の関数形を仮定した上 さらにモーメントを取ることで導いた連立方程式系(左)により記述され、計算が行われてきました。この手法では4つの複雑な常微分方程式を解かなければなりません。 それに対して、私たちは2つの常微分方程式と1つの代数方程式だけでほぼ同一の結果が得られる方程式系(右)を導きました。しかも、粒度分布関数の関数形を仮定する必要もなく、従来のものと比べて簡潔なのは一目瞭然です。計算機資源の節約や計算時間の短縮にもつながります。 この数学モデルの応用範囲は広く、ナノ粒子創製プロセスの予測計算のみならず、例えば蒸気タービン内における水滴発生(しばしばエロージョン(侵食)が問題となる)の計算や、雲や霧の発生といった気象分野に関わる問題、湿度コントロールが重要な建物の空間設計など、様々な分野の一助となることが期待できます。 また上記は自由分子領域での方程式系ですが、論文では連続領域における方程式系も導いてます。 ※ 詳しくはこちら(↓)をご参照ください。 Modelling and Simulation in Materials Science and Engineering, Vol. 20, No. 4, (May, 2012), pp. 045017 (11 pages). Valerian A. Nemchinsky and Masaya Shigeta IEEJ Transactions on Electrical and Electronic Engineering, Vol. 14, (January 1, 2019), pp. 16-28. Masaya Shigeta Plasma Chemistry and Plasma Processing, Vol. 40, Issue 3, (May 1, 2020), pp. 775-794. Masaya Shigeta 【 New!! 】3次元シミュレーションの結果は → こちら |
動画をクリックすると再生します
熱プラズマプロセスにおける二元系ナノ粒子群(ナノパウダー)の集団成長過程
|
熱プラズマプロセスにおけるシリサイド(ケイ化物:金属-シリコン間化合物)ナノ粒子群(ナノパウダー)の集団成長過程の計算予測結果です。 シリサイドのナノ粒子は、熱プラズマ下流(温度が3000度から1000度くらいまで一気に降下する)領域で均一核生成・不均一凝縮・粒子間凝集を経て形成すると考えられていますが、現象が数十ミリ秒で完了してしまうため(他にも理由はいろいろありますが)実験によって直接調べることは今のところ出来ていません。しかもナノ粒子群は集団的に振る舞いながら、さらに飽和蒸気圧の異なる複数の物質が共凝縮するという非常に複雑な過程ですので、理論や数値計算でも解析することは不可能でした。 そこで この問題を打開するために“Gibbs-Thomson効果による凝固点降下”および“二成分核生成理論・二成分凝縮理論”を組み込んだナノ粒子群形成の新しい数理モデル(方程式系)を構築しました。しかし この方程式系は従来の計算手法では解くことができないので、さらに「2方向ノーダル解法」という計算手法も独自に考案し、数値的に解くことを試みました。その結果、これまで想像の域を超えず未解明であったシリサイドナノ粒子群の集団的な成長過程を具体的に捉えることに世界で初めて成功しました。 モリブデンとシリコンの混合系(初期蒸気混合比 Mo:Si = 1:1 )の場合、まずモリブデンを主成分とするナノ粒子群が生成し、それからシリコンの凝縮によりが急成長していく様子が見て取れます。 一方でコバルトとシリコンの混合系(初期蒸気混合比 Co:Si = 1:1 )の場合、シリコンを主成分とするナノ粒子群が生成するや否や、コバルトとシリコンが同時に共凝縮しナノ粒子群が形成されていくことがわかります。 どちらの系においても、直径10nm程度、Si分率=50at.% のナノ粒子が多く形成されますが、初期蒸気混合比として 金属:シリコン=1:1というシンプルな条件を与えているにも関わらず、形成されるナノ粒子は大きさ・組成どちらもかなりの幅を持ってしまうことが、この計算によって明らかとなりました。 なお、創製されたナノ粒子群の最終形態だけは実験によって調べることができますので、その実験データと今回の計算結果を比較してみましたところ、両者は良く一致し、今回の新しいモデルと計算手法は妥当であることが示されています。 また同モデルと計算手法を用いて、上記のモリブデンシリサイド(Mo-Si)やコバルトシリサイド(Co-Si)の他に、チタンシリサイド(Ti-Si)や鉄シリサイド(Fe-Si)、さらにはボライド(ホウ化物:金属-ホウ素間化合物)や合金(Fe-Co, Fe-Nd等の磁性材料)のナノ粒子群形成過程の計算予測も進めています。 ※ 詳しくはこちら(↓)をご参照ください。 Journal of Applied Physics, Vol. 108, Issue 4, (August, 2010), pp. 043306 (15 pages). Masaya Shigeta and Takayuki Watanabe Powder Technology, Vol. 288, (January 1, 2016), pp. 191-201. Masaya Shigeta, Takayuki Watanabe Nanomaterials, Vol. 6, (March 7, 2016), pp. 43 (10 pages). (Impact factor = 3.553, 5-year impact factor = 4.100) Masaya Shigeta, Takayuki Watanabe |
動画をクリックすると再生します
対向流により急冷される高周波誘導結合型熱プラズマ流およびナノ粒子群生成
|
材料蒸気(ここでは白金蒸気)を含む熱プラズマ流を対向流によって急冷することで 核生成を促進しナノ粒子群を一気に大量生成することが可能となります。 定常2次元軸対称の条件下で、プラズマ流 → 原料蒸発 → ナノ粒子群成長 という一連の物理現象を 「すべて統合した数理モデル」を解くことで初めて得ることができる数値計算結果です。 ナノ粒子は均一核生成・不均一凝縮によって生成・成長すると同時に、ブラウン運動などの影響でナノ粒子同士も衝突し凝集成長します。このような多数のナノ粒子の集団的な成長過程は、分子動力学では現在のコンピューター性能を以ってしても計算することができないので、エアロゾル動力学に基づく方程式によって現象を表現するのが有効です。しかし、その方程式も複雑で数値的にもそのまま解くことができませんので、統計学的手法と組み合わせることで解を得ることができました。なお計算には原料蒸気の輸送過程もさることながら、拡散・熱泳動・移流によるナノ粒子輸送現象も考慮されています。 プラズマ流と急冷ガスの衝突面で均一核生成により大量の小さなナノ粒子が生成します。小さなナノ粒子は流れによって下流へ流されていきますが、周りの蒸気が凝縮しますので成長して大きくなっていきます。また同時にナノ粒子間凝集によっても成長しますが、合体成長ですので粒子数は減少します。大きなナノ粒子ほど下流部に多く存在するものの、その数が少ないのはそのためです。 ※ 詳しくはこちら(↓)をご参照ください。 Journal of Applied Physics, Vol. 103, Issue 7, (April, 2008), pp. 074903 (15 pages). Masaya Shigeta and Takayuki Watanabe Thin Solid Films, Vol. 516. (May, 2008), pp. 4415-4422. Masaya Shigeta and Takayuki Watanabe 日本機械学会論文集B編, 第75巻, 第758号, (10月, 2009), pp. 2019-2028. 茂田 正哉, 渡辺 隆行 |
動画をクリックすると再生します
ティグ溶接中のアークプラズマ
|
ティグ溶接中のアークプラズマのシミュレーション例です。 電極の下で最高温度が 18000 K を超えています。また最高速度は 200 m/s 程に達しています。 しかし、それらの位置は一致しておらず、また高温領域のサイズと高速領域のサイズが異なっていることも興味深い特徴です。 室温で上部から供給されたシールドガスの一部がアークプラズマに引き込まれて電離し、自らもアークプラズマになります。アークプラズマの高温領域はほとんど定常的ですが、中低温領域には流体力学的な不安定性によって非定常的な揺らぎが生じます。 ※ 詳しくはこちら(↓)をご参照ください。 Nanomaterials, Vol. 9, No. 12, (December 6, 2019), pp. 1736 (13 pages). (OPEN ACCESS) Masaya Shigeta, Manabu Tanaka, Emanuele Ghedini |
動画をクリックすると再生します
一様磁場における2つの非中性プラズマリングの運動
|
一様磁場における2つの非中性プラズマリングの運動を離散渦法でモデル化してシンプレクティック数値積分法をつかって、シミュレートしてみました。ここでは 非中性プラズマとして 電子プラズマ や 陽電子プラズマ を想定しています。一応 有限Larmor半径効果 や 電場の時間変化の効果 も考慮されています。色はそれぞれの系における速さを表しています。3回ループします。 |
動画をクリックすると再生します
高周波誘導熱プラズマと軸ずれ直流熱プラズマジェットの融合と渦生成のダイナミクス
|
ナノ粒子の大量生成を実現できる直流−高周波誘導ハイブリッド熱プラズマと非電離気体の共存系の電磁熱流体シミュレーションを行いました。室温〜1万度超という温度の時空間変化にともなって物性値と密度が数桁にわたり変化する低マッハ数の非圧縮性流れを同一計算領域内で解くという過酷な数値計算条件においても,流体力学的な不安定性の捕捉と数値安定的な長時間計算を両立できる手法を開発し,その熱流動場と渦構造のダイナミクスを捉えることに成功しました。高温のプラズマ域には大きな渦のみが存在し,小さな渦群は低温域にのみ生じる,という理論予測と一致する傾向が現れており,中心軸のずれた直流プラズマジェットと高周波誘導プラズマが衝突して合併した後に渦構造がさらに複雑なものに変遷していく様子が捉えられています。 ※ 詳しくはこちら(↓)をご参照ください。 Japanese Journal of Applied Physics, Vol. 62, (June 16, 2023), pp. SL0801. (OPEN ACCESS) Masaya Shigeta Journal of Physics D: Applied Physics, Vol. 49, No. 49, (November 9, 2016), pp. 493001 (18 pages). Masaya Shigeta Journal of Physics D: Applied Physics, Vol. 46, No. 1, (January, 2013), pp. 015401 (12 pages). Masaya Shigeta Plasma Sources Science and Technology, Vol. 21, No. 5, (October, 2012), pp. 055029 (14 pages). Masaya Shigeta |
動画をクリックすると再生します
プラズマジェット噴出時の熱流動ダイナミクスとナノ粒子雲の振舞い
|
Si蒸気を含んだ絶対温度12000KのArプラズマジェットが室温300Kの非電離Ar気体中に噴出する共存系のシミュレーションです。両者の相互作用による熱流動場の複雑なダイナミクスと 3000K/mmほどの非常に高い温度勾配をもつ境界領域で生成するSiナノ粒子の雲によってケルビン・ヘルムホルツ不安定性による「揺らぎ」が可視化されています。 ※ 詳しくはこちら(↓)をご参照ください。 Japanese Journal of Applied Physics, Vol. 62, (June 16, 2023), pp. SL0801. (OPEN ACCESS) Masaya Shigeta Plasma Chemistry and Plasma Processing, Vol. 40, Issue 3, (May 1, 2020), pp. 775-794. Masaya Shigeta |
© 2004- Masaya SHIGETA